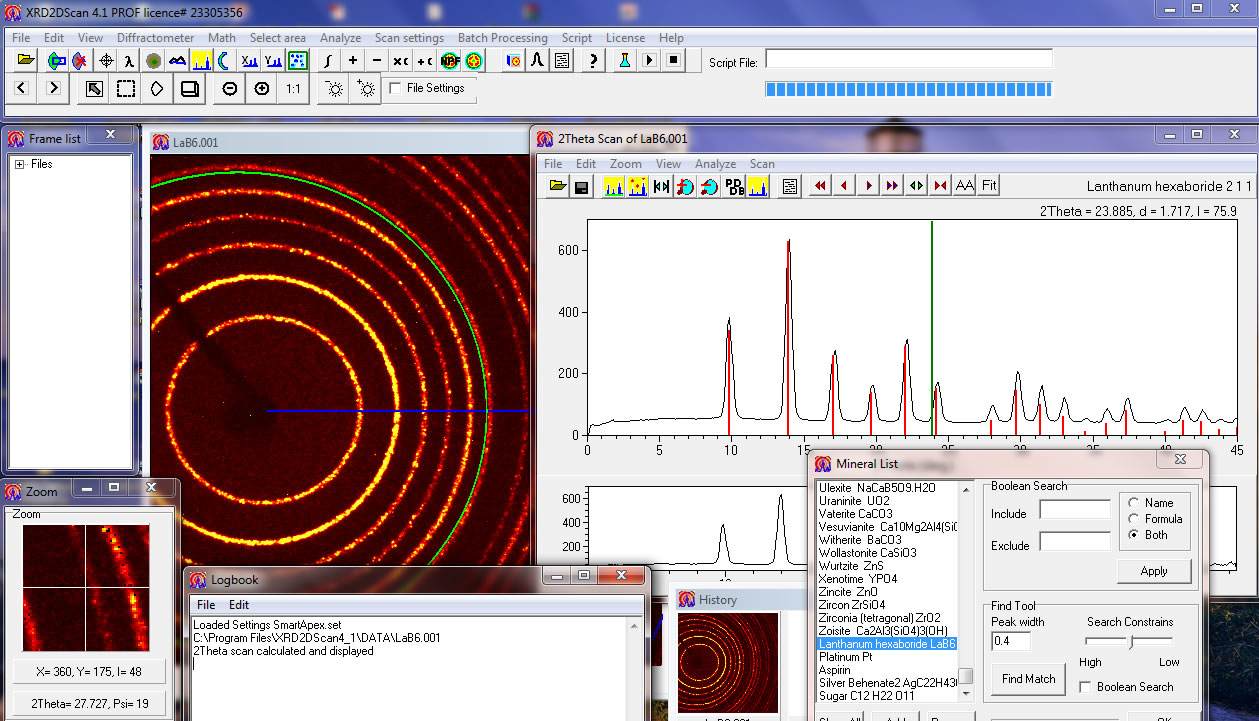
HighScore is the ideal software for phase identification, semi-quantitative phase analysis, pattern treatment, profile fitting and more. The software package. Is an easy-to-use software for phase identification from powder diffraction data. It compares the diffraction pattern of your sample to a database containing reference patterns in order to identify the phases which are present. Additional knowledge about the sample like known phases, elements or density can be applied easily.

Max von Laue, in 1912, discovered that crystalline substances act as three-dimensional diffraction gratings for X-ray wavelengths similar to the spacing of planes in a crystal lattice. X-ray diffraction is now a common technique for the study of crystal structures and atomic spacing.X-ray diffraction is based on constructive interference of monochromatic X-rays and a crystalline sample.

These X-rays are generated by a cathode ray tube, filtered to produce monochromatic radiation, collimated to concentrate, and directed toward the sample. The interaction of the incident rays with the sample produces constructive interference (and a diffracted ray) when conditions satisfy ( n λ=2 d sin θ). This law relates the wavelength of electromagnetic radiation to the diffraction angle and the lattice spacing in a crystalline sample.

Our drag-and-drop Form Builder also makes it easy to update application questions, customize the template design, and add your logo for a professional touch. New jersey driver license application form ba 208.

These diffracted X-rays are then detected, processed and counted. By scanning the sample through a range of 2 θangles, all possible diffraction directions of the lattice should be attained due to the random orientation of the powdered material.

Conversion of the diffraction peaks to d-spacings allows identification of the mineral because each mineral has a set of unique d-spacings. Typically, this is achieved by comparison of d-spacings with standard reference patterns.All diffraction methods are based on in an X-ray tube. These X-rays are directed at the sample, and the diffracted rays are collected. A key component of all diffraction is the angle between the incident and diffracted rays. Powder and single crystal diffraction vary in instrumentation beyond this. X-ray Powder Diffraction (XRD) Instrumentation - How Does It Work? X-ray powder diffractogram.

Peak positions occur where the X-ray beam has been diffracted by the crystal lattice. The unique set of d-spacings derived from this patter can be used to 'fingerprint' the mineral.The geometry of an X-ray diffractometer is such that the sample rotates in the path of the collimated X-ray beam at an angle θ while the X-ray detector is mounted on an arm to collect the diffracted X-rays and rotates at an angle of 2 θ. The instrument used to maintain the angle and rotate the sample is termed a goniometer. For typical powder patterns, data is collected at 2 θ from 5 ° to 70 °, angles that are preset in the X-ray scan.

X-ray powder diffraction is most widely used for the identification of unknown crystalline materials (e.g. Minerals, inorganic compounds). Homogeneous and single phase material is best for identification of an unknown. Must have access to a standard reference file of inorganic compounds (d-spacings, hkls). Requires tenths of a gram of material which must be ground into a powder.

For mixed materials, detection limit is 2% of sample. For unit cell determinations, indexing of patterns for non-isometric crystal systems is complicated. Peak overlay may occur and worsens for high angle 'reflections'User's Guide - Sample Collection and Preparation. Data Collection The intensity of diffracted X-rays is continuously recorded as the sample and detector rotate through their respective angles. A peak in intensity occurs when the mineral contains lattice planes with d-spacings appropriate to diffract X-rays at that value of θ. Although each peak consists of two separate reflections (K α 1 and K α 2), at small values of 2 θ the peak locations overlap with K α 2 appearing as a hump on the side of K α 1. Greater separation occurs at higher values of θ.

Typically these combined peaks are treated as one. The 2 λ position of the diffraction peak is typically measured as the center of the peak at 80% peak height. Data ReductionResults are commonly presented as peak positions at 2 θ and X-ray counts (intensity) in the form of a table or an x-y plot (shown above).

Intensity ( I) is either reported as peak height intensity, that intensity above background, or as integrated intensity, the area under the peak. The relative intensity is recorded as the ratio of the peak intensity to that of the most intense peak ( relative intensity = I/I 1 x 100 ). Determination of an UnknownThe d-spacing of each peak is then obtained by solution of the Bragg equation for the appropriate value of λ.

Once all d-spacings have been determined, automated search/match routines compare the ds of the unknown to those of known materials. Because each mineral has a unique set of d-spacings, matching these d-spacings provides an identification of the unknown sample. A systematic procedure is used by ordering the d-spacings in terms of their intensity beginning with the most intense peak. Files of d-spacings for hundreds of thousands of inorganic compounds are available from the as the Powder Diffraction File (PDF). Many other sites contain d-spacings of minerals such as the.

Commonly this information is an integral portion of the software that comes with the instrumentation. Determination of Unit Cell DimensionsFor determination of unit cell parameters, each reflection must be indexed to a specific hkl. LiteratureThe following literature can be used to further explore X-ray Powder Diffraction (XRD). Bish, DL and Post, JE, editors. Modern Powder Diffraction. Reviews in Mienralogy, v.

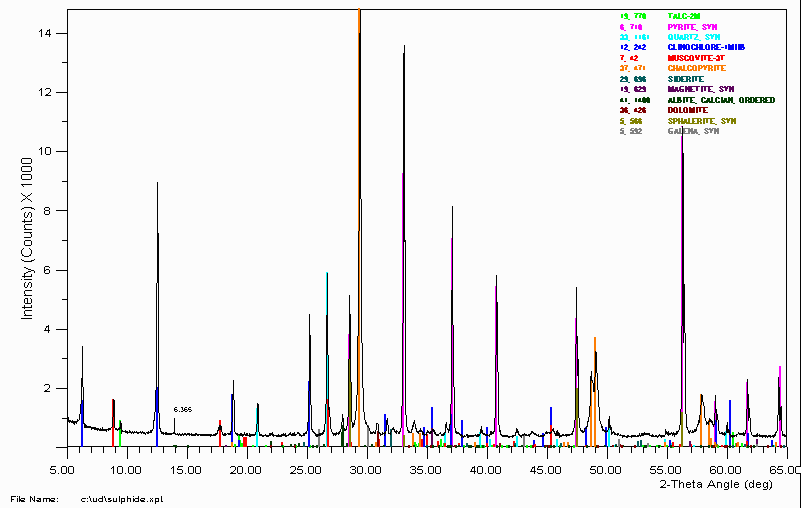
Mineralogical Society of America. Cullity, B. Elements of X-ray diffraction.

Addison-Wesley, Reading, Mass. Klug, H. X-ray diffraction procedures for polycrystalline and amorphous materials. Wiley, New York.

Moore, D. Reynolds, Jr. X-Ray diffraction and the identification and analysis of clay minerals. Oxford University Press, New York.Related LinksFor more information about X-ray Powder Diffraction (XRD) follow the links below.; Materials Research Lab, University of California- Santa Barbara.; an on-line journal that describes and demonstrates a wide range of applications using Xray diffraction.University of California, Santa Barbara.from LLNL.from Steve Nelson, Tulane University.part of the.

Use the 'Learn About' link to find animations of the structures of common molecules (including minerals), crystallography learning resources (tutorials, databases and software), resources on crystallization, and tutorials on symmetry and point groups.Teaching Activities and ResourcesTeaching activities, labs, and resources pertaining to X-ray Powder Diffraction (XRD). This problem develops skills in X-ray diffraction analysis as applied to clay mineralogy, reinforces lecture material on the geochemistry of weathering, and demonstrates the role of petrologic characterization in site engineering. (PowerPoint 1.6MB Sep7 07) by Melody Bergeron, at Montana State University. Brady, John B., and Boardman, Shelby J., 1995, Introducing Mineralogy Students to X-ray Diffraction Through Optical Diffraction Experiments Using Lasers. Education, v. 43 #5, 471-476.

Brady, John B., Newton, Robert M., and Boardman, Shelby J., 1995, New Uses for Powder X-ray Diffraction Experiments in the Undergraduate Curriculum. Education, v. 43 #5, 466-470. Dutrow, Barb, 1997, Better Living Through Minerals X-ray Diffraction of Household Products, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p.

349-359. Hovis, Guy, L., 1997, Determination of Chemical Composition, State of Order, Molar Volume, and Density of a Monoclinic Alkali Feldspar Using X-ray Diffraction, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 107-118. Brady, John B., 1997, Making Solid Solutions with Alkali Halides (and Breaking Them), in: Brady, J., Mogk, D., and Perkins D.

(eds.) Teaching Mineralogy, Mineralogical Society of America, p. 91-95. Perkins, Dexter, III, and Sorensen, Paul, Mineral Synthesis and X-ray Diffraction Experiments, in: Brady, J., Mogk, D., and Perkins D. (eds.) Teaching Mineralogy, Mineralogical Society of America, p. 81-90. Hollecher, Kurt, A Long-Term Mineralogy Practical Exam, in: Brady, J., Mogk, D., and Perkins D.

(eds.) Teaching Mineralogy, Mineralogical Society of America, p. 43-46. Hluchy, M.M., 1999, The Value of Teaching X-ray Techniques and Clay Mineralogy to Undergraduates, Jour. Geoscience Education, v.

The quantification of clay minerals is essential for the evaluation of clay-rich rock and soil, but it remains challenging due to the unique structures and various element compositions of clay minerals. In this article, several quantification methods for clay minerals sourced from X-ray diffraction (XRD) analysis, mainly recommending the reference intensity ratio (RIR), mineral intensity factor (MIF), Rietveld, and full pattern summation methods are reviewed. Principles and applications of these methods are focused upon in addition to related differences in the analysis of clay minerals (i.e., sample preparation, the selection of characteristic reflections for quantification and standards added during analysis). This critical review also provides a proposal for selection of an adaptive XRD quantification method to be applied to various clay-rich samples.

Previous article in issue. Next article in issue.